Home About Downloads GPF-EP Citation Contact
Instituto de Química UFRJ

Generalized Product Function Energy Partitioning

Chemical bonding is the result of modifications in the electronic density caused by Quantum Interference. Interference Energy Analysis leads to a unified view of the chemical bond.

What is GPF-EP?

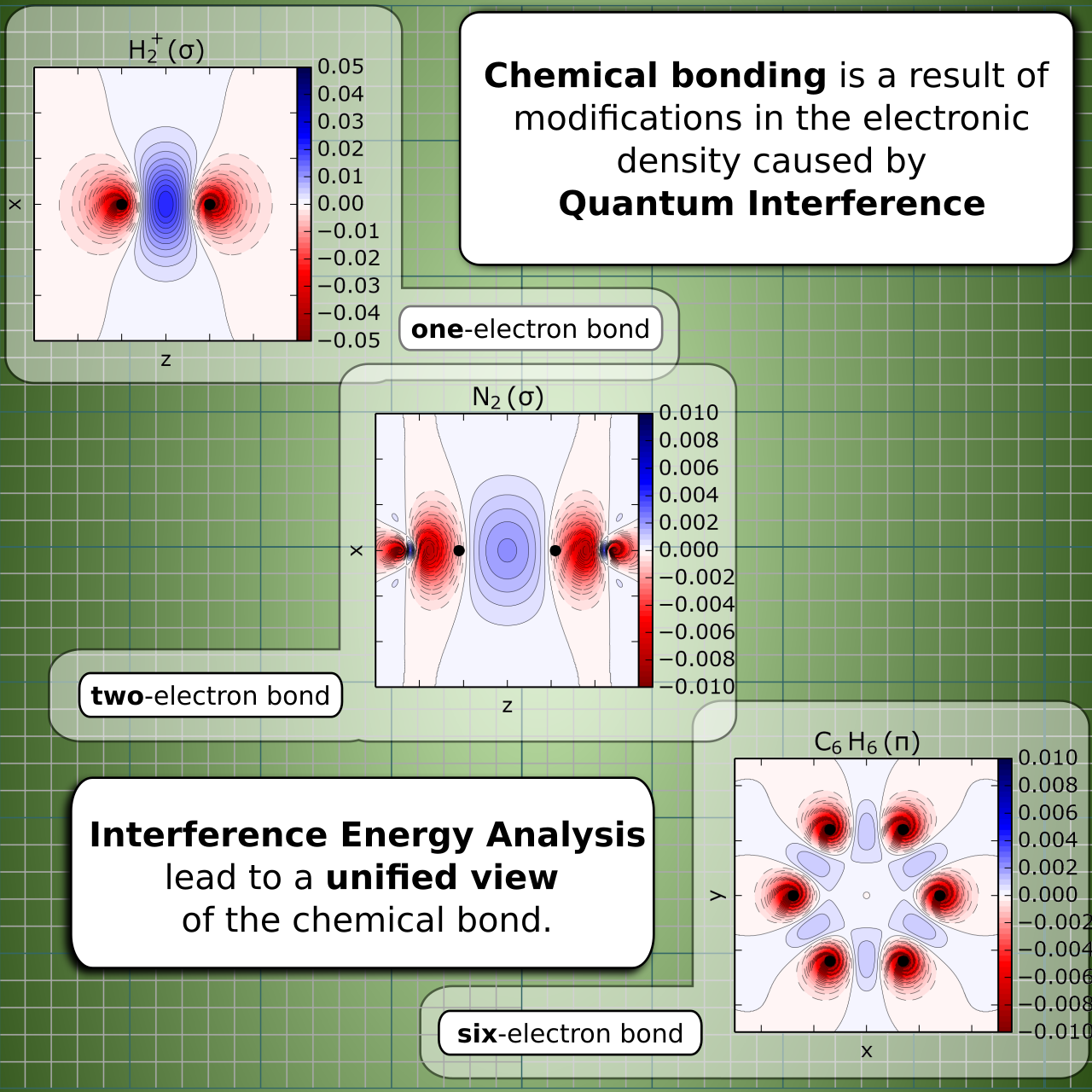
In simple words, the Generalized Product Function Energy Partitioning (GPF-EP) is a powerful Energy Decomposition Analysis (EDA) scheme suited for studying the nature of the chemical bond in molecular systems. The method is grounded on the original density-based energy decomposition first proposed by Ruedenberg [1]. Electronic densities are separated in a “quasi-classical” part, which can be mostly interpreted classically, and an interference part, which accounts for quantum interference between one-electron eigenstates. An analogous separation can be made for the electronic energy:

\rho = \rho_QC + \rho_INT

E = E[QC] + E[INT]

GPF-EP is an adaptation of Rudenberg’s original framework to the GPF wave functions, developed by Roy McWeeny [2]. A GPF wave function consists of a strongly orthogonal product of smaller wave functions of electron subspaces (groups) of a molecular system, and its reduced density matrices (RDMs) consist of intergroup and intragroup parts. This particular structure of the RDMs of GPF wave functions allows the energy partitioning to be carried out for individual bonds and bond groups. The interpretation of the results is facilitated by the use of modern VB functions such as the Spin Coupled Generalized Valence Bond (SCGVB) [3,4], since that method naturally generate uniquely determined quasi-atomic orbitals, allowing direct correspondence between results and chemical structures (atoms connected by chemical bonds). This choice of group wave functions also precludes the selection of criteria for atomic orbital generation, which was somewhat arbitrary in Ruedenberg's original work.

About the Program

At the present version (1.0), the GPF-EP program exists as a subprogram of the GAMESS / VB2000 (3.0) code. It is planned to be fully integrated to VB2000 in the next version (3.1).

GPF-EP allows to partition the total energy of an atomic or molecular system into two main contributions, the quasi-classical energy, E[QC] and the interference energy, E[INT]. The GPF wave function allows the partition to be made for each electron group in a GPF wave function, which can be associated to properties of specific parts in a molecule (specific chemical bonds, lone pais, etc.).

There is also an implemented feature in the GPFEP program to partition the electric dipole moment of a molecule in the quasi-classical and interference contributions for each electron group (see reference 16 for further details).

Acknowledgements

The GPF-EP Authors (Thiago M. Cardozo, David W.O. de Sousa, Carlos E. V. Moura, and Marco A. C. Nascimento) are grateful to the Brazilian financial support agencies CAPES, CNPQ and FAPERJ.

The GPF-EP Program was originally written as part of TMC’s PhD thesis and further developed in DWOS’ MSc project. Besides the authors mentioned above, the following people have also contributed in this project: Gabriel Freitas Nascimento, Francisco Senna Vieira, and Felipe Fantuzzi.

GPFPlot

GPF-PLOT is a Python script which generates 2D plots of orbitals, electronic densities and GPF density partitioning associated to VB2000 output files. It is available for download on GitHub.

More Information

GPF-EP original paper: Cardozo, T. M.; Nascimento, M. A. C. Energy partitioning for generalized product functions: The interference contribution to the energy of generalized valence bond and spin coupled wave functions. J. Chem. Phys., 2009 130 (10) 104102. DOI: 10.1063/1.3085953

GPF-EP mini review: Fantuzzi, F.; Sousa, D. W. O. de; Nascimento, M. A. C. The Nature of the Chemical Bond from a Quantum Mechanical Interference Perspective. ChemistrySelect, 2017, 2 (2), 604–619. DOI: 10.1002/slct.201601535

GPF-EP Book Chapter and Tutorial: Cardozo, T. M.; Sousa, D. W. o. de; Fantuzzi, F.; Bitzer, R. S.; Nascimento, M. A. C. The Chemical Bond as a Manifestation of Quantum Mechanical Interference: Theory and Applications of the Interference Energy Analysis using SCGVB wave functions. In S. Shaik and P.C. Hiberty (eds.), Valence Bond, Elsevier, 2022. To be published.

GPF-EP Tutorial: Cardozo, T. M.; Sousa, D. W. o. de; Nascimento, M. A. C. The Quantum Interference Energy Analysis: A Tutorial. In S. Shaik and P.C. Hiberty (eds.), Valence Bond, Elsevier, 2022. To be published.

Also see a full list of the GPF-EP publications below.

References

    Theory:

  1. Ruedenberg, K. The Physical Nature of the Chemical Bond. Rev. Mod. Phys. 1962, 34, 326–376. DOI: 10.1103/RevModPhys.34.326
  2. McWeeny, R. The density matrix in many-electron quantum mechanics I. Generalized product functions. Factorization and physical interpretation of the density matrices. Proc. R. Soc. A 1959, 253, 242–259. DOI: 10.1098/rspa.1959.0191
  3. Goddard, W. Improved Quantum Theory of Many-Electron Systems. I. Construction of Eigenfunctions of Ŝ² Which Satisfy Pauli's Principle. Phys. Rev. 1967, 157, 73–80; ibid., 81–93. DOI: 10.1103/PhysRev.157.73
  4. Gerratt, J.; Lipscomb, W. N. Spin-coupled wave functions for atoms and molecules.Proc. Natl. Acad. Sci. USA 1968, 59, 332–335. DOI: 10.1073/pnas.59.2.332

    5. GPF-EP publications (updated Oct 16th, 2021):

  5. Cardozo, T. M.; Nascimento, M. A. C. Energy partitioning for generalized product functions: The interference contribution to the energy of generalized valence bond and spin coupled wave functions. J. Chem. Phys., 2009 130 (10) 104102. DOI: 10.1063/1.3085953
  6. Cardozo, T. M.; Nascimento, M. A. C. Chemical Bonding in the N2 Molecule and the Role of the Quantum Mechanical Interference Effect. J. Phys. Chem. A, 2009, 113 (45), 12541–12548. DOI: 10.1021/jp903963h
  7. Cardozo, T. M.; Nascimento Freitas, G.; Nascimento, M. A. C. Interference effect and the nature of the π-bonding in 1,3-butadiene. J. Phys. Chem. A, 2010, 114 (33), 8798–8805. DOI: 10.1021/jp101785p
  8. Fantuzzi, F.; Cardozo, T. M.; Nascimento, M. A. C. The role of quantum-mechanical interference and quasi-classical effects in conjugated hydrocarbons. Phys. Chem. Chem. Phys., 2012, 14 (16), 5479–88. DOI: 10.1039/c2cp24125k
  9. Vieira, F. S.; Fantuzzi, F.; Cardozo, T. M.; Nascimento, M. A. C. Interference energy in C-H and C-C bonds of saturated hydrocarbons: Dependence on the type of chain and relationship to bond dissociation energy. J. Phys. Chem. A, 2013, 117 (19), 4025–4034. DOI: 10.1021/jp4005746
  10. Cardozo, T. M.; Fantuzzi, F.; Nascimento, M. A. C. The non-covalent nature of the molecular structure of the benzene molecule. Phys. Chem. Chem. Phys., 2014, 16 (22), 11024. DOI: 10.1039/c3cp55256j
  11. Fantuzzi, F.; Nascimento, M. A. C. Description of polar chemical bonds from the quantum mechanical interference perspective. J. Chem. Theor. Comput., 2014, 10 (6), 2322–2332. DOI: 10.1021/ct500334f
  12. Fantuzzi, F.; Cardozo, T. M.; Nascimento, M. A. C. Nature of the Chemical Bond and Origin of the Inverted Dipole Moment in Boron Fluoride: A Generalized Valence Bond Approach. J. Phys. Chem. A, 2015, 119 (21), 5335–5343. DOI: 10.1021/jp510085r
  13. Sousa, D. W. O. de; Nascimento, M. A. C. Is There a Quadruple Bond in C2? J. Chem. Theor. Comput., 2016, 12 (5), 2234–2241. DOI: 10.1021/acs.jctc.6b00055
  14. Fantuzzi, F.; Cardozo, T. M.; Nascimento, M. A. C. The Nature of the Singlet and Triplet States of Cyclobutadiene as Revealed by Quantum Interference. ChemPhysChem, 2016, 17 (2), 288–295. DOI: 10.1002/cphc.201500885
  15. Fantuzzi, F.; Sousa, D. W. O. de; Nascimento, M. A. C. The Nature of the Chemical Bond from a Quantum Mechanical Interference Perspective. ChemistrySelect, 2017, 2 (2), 604–619. DOI: 10.1002/slct.201601535
  16. Fantuzzi, F.; Sousa, D. W. O. de; Nascimento, M. A. C. Chemical bonding in the pentagonal-pyramidal benzene dication and analogous isoelectronic hexa-coordinate species. Comput. Theor. Chem., 2017, 1116), 225–233. DOI: 10.1016/j.comptc.2017.03.020
  17. Fantuzzi, F.; Cardozo, T. M.; Nascimento, M. A. C. On the metastability of doubly charged homonuclear diatomics. Phys. Chem. Chem. Phys., 2017, 19 (29), 19352–19359. DOI: 10.1039/C7CP02792C
  18. Sousa, D. W. O. de; Nascimento, M. A. C. Are One-Electron Bonds Any Different from Standard Two-Electron Covalent Bonds? Acc. Chem. Res., 2017, 50 (9), 2264–2272. DOI: 10.1021/acs.accounts.7b00260
  19. Sousa, D. W. O. de; Nascimento, M. A. C. Quantum Interference Contribution to the Dipole Moment of Diatomic Molecules. J. Phys. Chem. A, 2018, 122 (5), 1406–1412. DOI: 10.1021/acs.jpca.7b11760
  20. Fantuzzi, F.; Wolff, W.; Quitián-Lara, H. M.; Boechat-Roberty, H. M.; Hilgers, G.; Rudek, B.; Nascimento, M. A. C. Unexpected reversal of stability in strained systems containing one-electron bonds. Phys. Chem. Chem. Phys., 2019, 21 (45), 24984–24992, 2019. DOI: 10.1039/C9CP04964A
  21. Sousa, D. W. O. de; Nascimento, M. A. C. One-electron bonds are not “half-bonds”. Phys. Chem. Chem. Phys., 2019, 21 (24), 13319–13336. DOI: 10.1039/C9CP02209K
  22. Sousa, D. W. O. de; Nascimento, M. A. C. Three-center two-electron bonds in the boranes B2H6 and B3H8− from the quantum interference perspective. Theor. Chem. Acc., 2020, 139 (8), 140. DOI: 10.1007/s00214-020-02654-4
  23. Sousa, D. W. O. de; Nascimento, M. A. C. Substituent Effects on the Quantum Interference of Two-Center One-Electron Bonds: [B 2X6]− (X = H, F, Cl, CN, OH, CH3, and OCH3). J. Phys. Chem. A, 2021, 125 (21), 4558–4564. DOI: 10.1021/acs.jpca.1c02771
  24. Sousa, D. W. O. de; Nascimento, M. A. C. Three-center two-electron bonding from the quantum interference perspective. To be published.